Casadirectx 12x

1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =

Por um escritor misterioso
Last updated 03 novembro 2024
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
HELP! ONLY IF YOU KNOW THE ANSWER also this goes with the other question I asked Write the standard
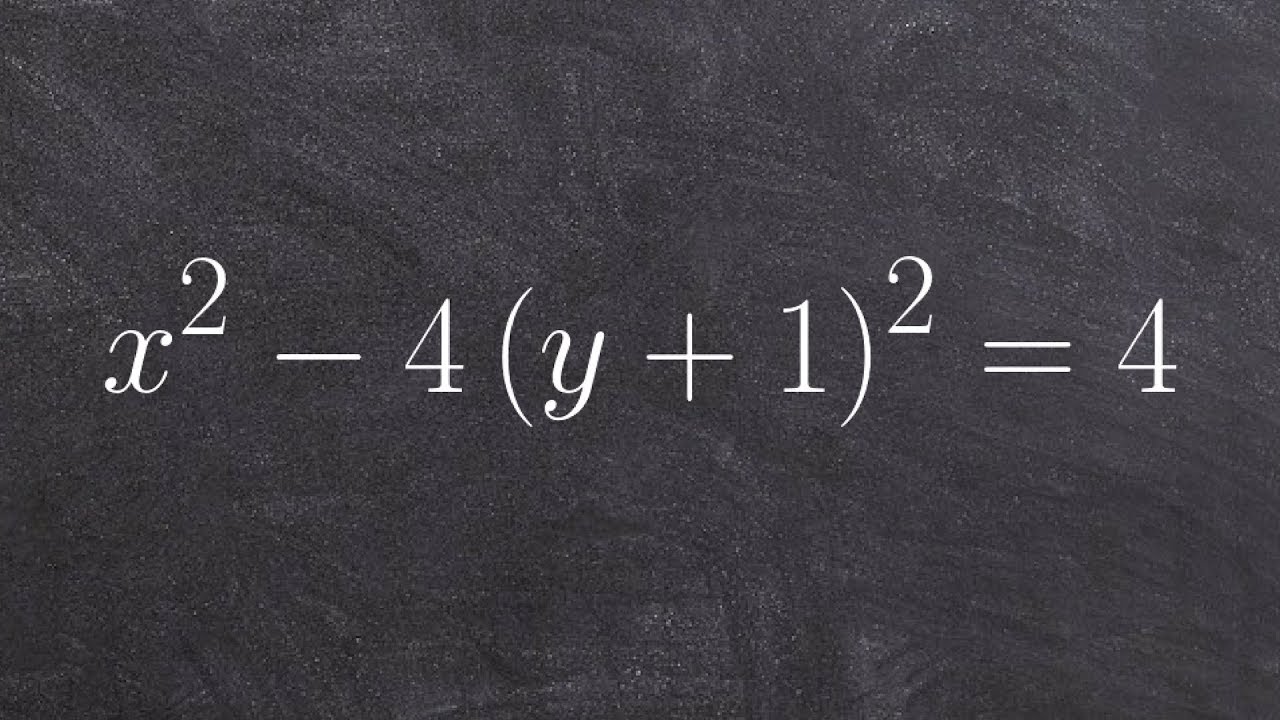
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
how to sketch the graph of a hyperbola in conic sections
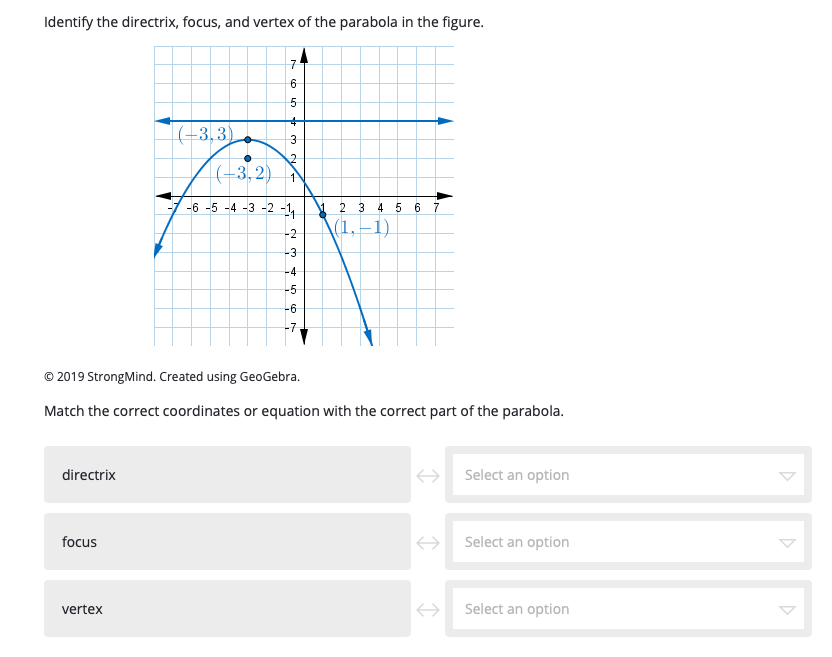
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Answered: Identify the directrix, focus, and…
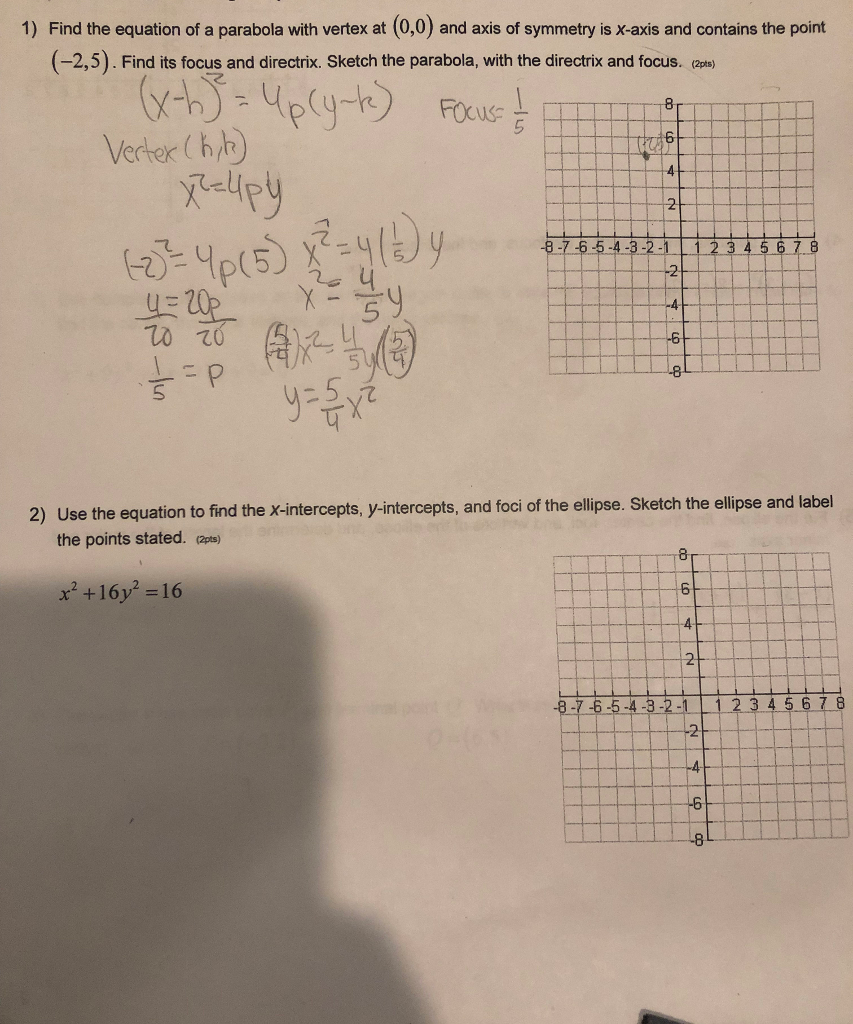
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Solved Find the equation of a parabola with vertex at (0,0)
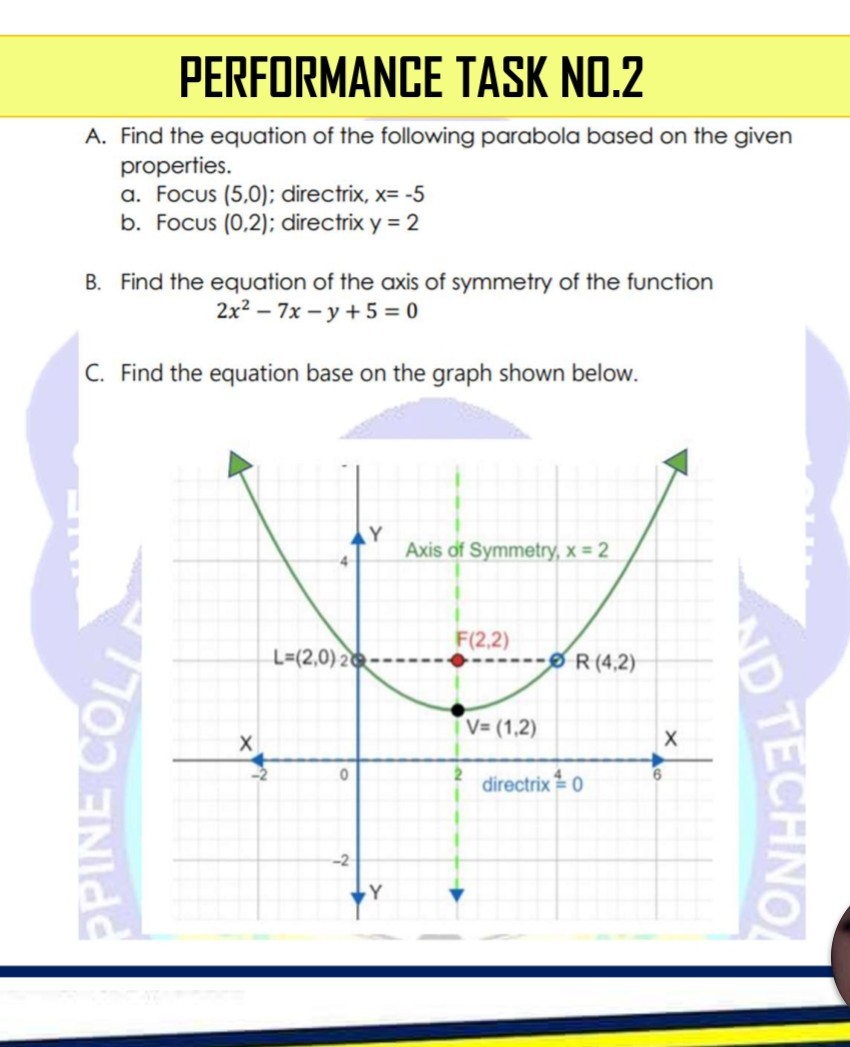
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
SOLVED: PERFIRMANCE TASK NU.2 A. Find the equation of the following parabola based on the given properties. a. Focus (5,0); directrix, x=-5 b. Focus (0,2); directrix y=2 B. Find the equation of
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Find the vertex, focus, and directrix of each parabola. Grap
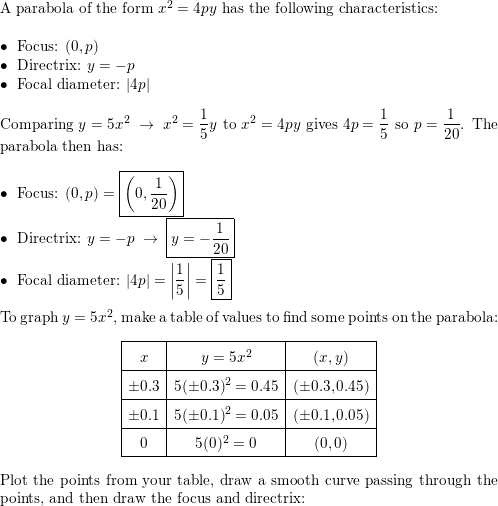
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Find the focus, directrix, and focal diameter of the parabol
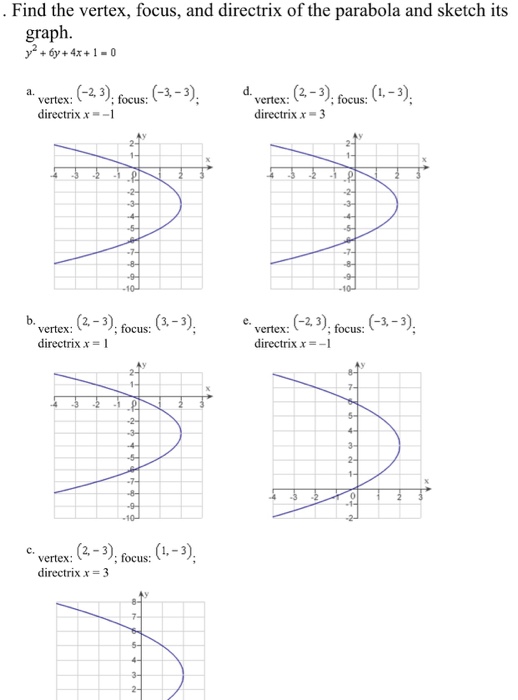
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Solved Find the vertex, focus, and directrix of the parabola
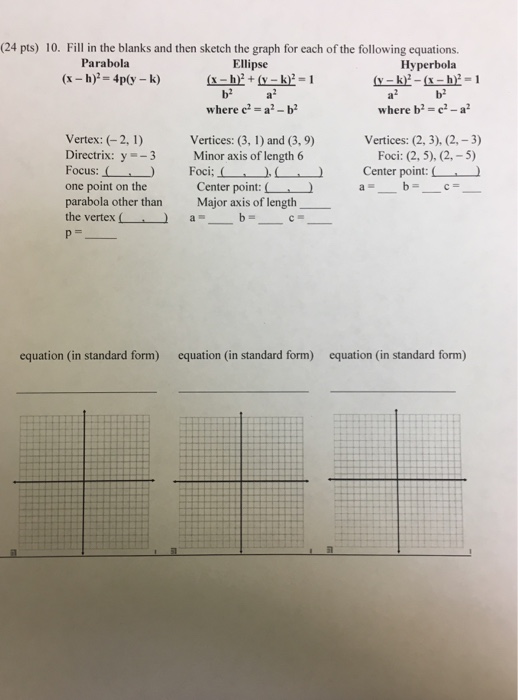
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Solved Fill in the blanks and then sketch the graph for each
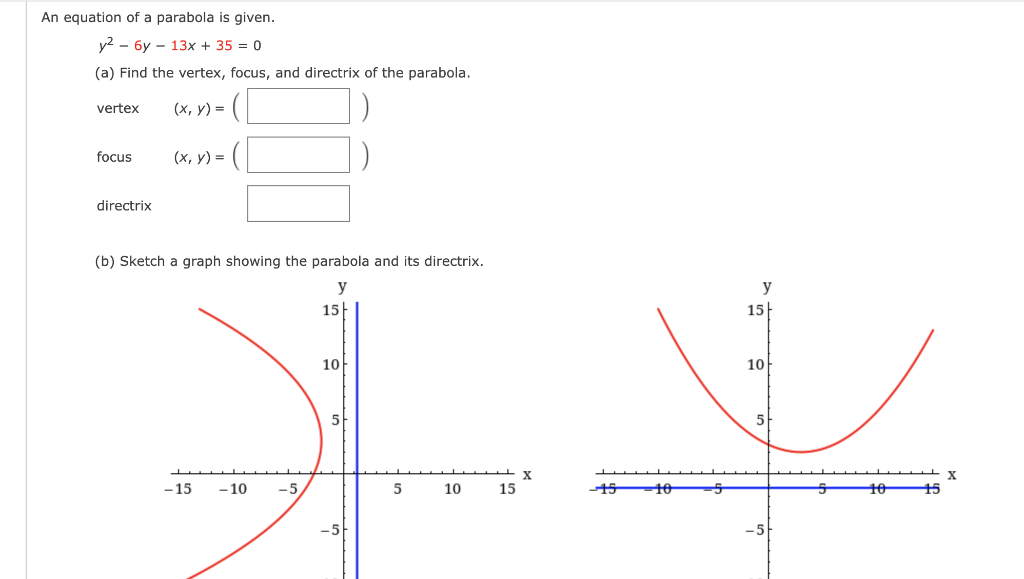
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Solved An equation of a parabola is given. y2−6y−13x+35=0
1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Conic sections: Analyzing Conic Sections with the Algebraic Method - FasterCapital
Recomendado para você
você pode gostar

© 2014-2024 faktorgumruk.com. All rights reserved.